Puzzle 419: KenKen

As perhaps one of the worst years humankind has ever seen leads to another one, here is a kenken. 

To retain the theme, some cells are not caged. However, that should not discourage you, as this one  has a near clean solving path. 

Puzzle 418: Blockchain Kakuro

This is a Blockchain Kakuro.

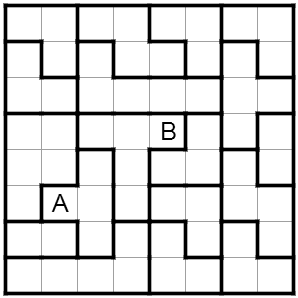
Puzzle 417: Cipher Tapa

Rules: Paint some squares to create a continuous wall of connected squares. Number(s) in a square
indicates how many painted squares are contained in a continuous black cell block in its
surrounding cells. If there is more than one number in the square, there has to be at least one
white cell separating the black cell blocks. Painted squares cannot form a 2x2 square.
Numbered squares cannot painted. Numbers are replaced by letters. Each different letter
stands for a different number.

Puzzle 416: Heterogenous Loop

This is a new loop style.

Rules: Draw a closed loop that connects the centres of all cells horizontally or vertically.
The loop may not cross itself or branch off, and must turn in every circle. For each circle,
the sum of lengths of segments connecting the circle on either side has to be different.

Puzzle 415: Non-consecutive Fillomino

Rules: Divide the grid along the gridlines into several polyominoes, and fill each of the empty cells with a number. When two orthogonally adjacent cells belong to different polyominoes, they
cannot contain the same number. Given numbers represent the area of the polyomino they belong to. A polyomino may contain none, or one, or more of the givens. No two polyominoes of consecutive areas may share an edge.

Puzzle 414: Product Snake

Rules: Draw a snake one cell wide, that does not touch itself, not even diagonally. The head and tail are given as black cells. If a row/column contains a number outside, it represents the product of  lengths of all groups of contiguous snake cells in that row/column.

Puzzle 413: Fillomino

Rules: Divide the grid along the gridlines into several polyominoes, and fill each of the empty cells with a number. When two orthogonally adjacent cells belong to different polyominoes, they
cannot contain the same number. Given numbers represent the area of the polyomino they belong to. A polyomino may contain none, or one, or more of the givens.

Puzzle 412: Product Snake

Another new variation.

Rules: Draw a snake one cell wide, that does not touch itself, not even diagonally. The head and tail are given as black cells. If a row/column contains a number outside, it represents the product of  lengths of all groups of contiguous snake cells in that row/column.

Puzzle 411: Cascade Snake

This is a novel snake style.

Rules: Draw a snake one cell wide, that does not touch itself, not even diagonally. The head and tail are
given as circles. Numbers outside rows/columns indicate how many snake segments in that row/
column have at least one neighboring snake segment in a row/column that is different than the one it is contained in. To make it simpler, for example, if the snake occupies R5C5-C7, the cell R5C6 adds 1 to the total for that column.

 

Non-puzzle

       I grew up in the state that I am residing in, and to my utter and persisting annoyance, I keep struggling to get my second name(sometimes the first name too) spelled and pronounced correctly ever since I was as young as I remember! This is no short of a tragedy. I can't find a sane reason why this happens, except that the people involved are certainly too ignorant, apathetic, insensitive and sometimes uneducated, some of those attributes being so native to my place. When I don't, EVER, misspell or mispronounce anyone, and absolutely anyone, and at least made a sincere effort if I have ever failed, is that not obligatory on the part of every other person, no matter what ethnicity they belong to? As outrageous as it may seem, they write down a name that they think is a near match, something that is usually common and prevalent in the country.
      This personal grief, apart from being a source of frustration, has often taken larger dimensions as it permeates into legal territory where I am forced to run pillar to post to get bad documents fixed, despite spoon-fed spellings. Especially with the present ruling entity that has set a benchmark for 'legalized lies" and legalized terror , these paperwork and corrections are a reason for deeper anguish. Dreaming of a digitized, 2 billion strong nation is one thing, knowing that you have efficient workforce to do so, is another.
    I also disliked that a person from the puzzle community did not care to find out the correct pronunciation, thankfully not the spelling, before announcing my name at a national event.
   
   

Puzzle 410: Islands and Capitals

This is a new puzzle style.

Rules: Shade some cells black to leave some islands, each island being a group of contiguous white cells, and  containing no more than one blue shaded cell.  Shaded cells cannot make a 2x2 square anywhere in
the grid, and must all be connected horizontally or vertically in one group. Each island would contain one instance of the number that represents its area in cells, or the "capital", and two or more instances of other numbers, if any. A single cell island is not prohibited. Some or all capitals are already shaded blue.

Puzzle design contest

Puzzle enthusiasts can enter by sending a puzzle. Rules and constraints are listed below. To allow for a result, at least five entries would be required. Furthermore, entries will be published here after the submissions close without revealing the authors, for the entrants to solve, vote and decide a winner. Puzzles will be voted for such attributes like logical  path to arrive at the solution, and clue symmetry. Polling method will be announced at the same time as the publishing of entries, depending on the number of puzzles. This contest is open to all. Puzzles may be sent before 11:00 pm GMT, the 30th of November, to anuragthefirst at gmail dot com. Again, contest may remain undecided if very few entries are received.

The entry has to contain a "fusion" puzzle, rules follow.
Rules:  Divide the grid along the gridlines into polyominoes, so that no two polyominoes with the same area share an edge. Every cell must belong to one of the polyominoes. All numbers contained in a polyomino must repeat in that polyomino, except one number, that must be equal to the area of the polyomino, and appears exactly once in that polyomino. The above rule allows a polyomino of area equal to 1.

Constraints: 

1. The puzzle has to use a 10x10 rectangular grid. 

2. No given clue shall be equal to, or larger than the area of the largest polyomino/s. 

3. While the previous constraint forces at least one cell without a given, you may leave as many empty cells as you like, which may also aid in introducing symmetry.
4. The puzzle has to have a unique solution.
5. There is no restriction on clues, but trivial puzzles are strongly discouraged. For example, a puzzle with one '99', and 98 2s may be considered trivial by definition. 

Note: Not all empty cells are required to be filled in the solution. A puzzle is not considered non-unique if cells can be filled in multiple ways as long as the polyominoes are uniquely formed. This was not mentioned in the rules paragraph. 

Puzzle 409: SDD Sudoku

New.

Rules: Place...ce. Digits are replaced by alphabets. A digit outside indicates that it has to be placed as many cells away.

Puzzle 408: Marine Camping

Rules: Place the given fleet of ships into the grid. There is a tree for every ship. Ships may not touch each other, not even diagonally. Numbers outside indicate how many cells in the corresponding row or column are occupied by ship segments. Each ship should be placed beside its tree, such that the tree is adjacent to a dead-end segment of the ship.

Puzzle 407: Easy As ABC

If you manage to identify anything that may have been inadvertently hidden, be advised that it was probably only a coincidence, and is not supposed to be discussed outside the puzzle circuit.

Rules: Place each of the letters D,I,M,O, and T into the grid, one letter per cell, such that every row/column contains each letter once. Letters outside are the first seen in that direction.

.

Puzzle 406: Fusion

This is a fresh puzzle style.

Rules: Divide the grid along the gridlines into polyominoes, so that no two polyominoes with the same area share an edge. All numbers contained in a polyomino must repeat in that polyomino, except one number, that must be equal to the area of the polyomino, and appears exactly once in that polyomino. The above rule allows a polyomino of area equal to 1. 

Puzzle 405: Fourtified Sudoku

This is a new sudoku variation.

Rules: Place a digit in each cell, such that every row, column, and every thick outlined 3x3 box contains each digit 1 to 9 exactly once. Numbers outside indicate the sum of exactly 4 digits reachable in a single path through adjacent cells, starting with the cell adjacent to the number. No two paths are allowed to overlap or intersect.

Puzzle 404: Combinable Sudoku

This is a new sudoku variation.

Rules: Place a digit in each cell, such that every row, column, and 3x3 box contains each digit 1 to 9 exactly once. Small numbers in some cells are the least possible sum of the number contained in that cell, and any of the numbers sharing an edge. In other words, small numbers represent the lower sum threshold that restricts the range of adjacent numbers for the number in that cell.

Puzzle 403: Unparalleled Sudoku

A new sudoku variation.

Rules:   Place a digit in each cell, such that every row, column, and 3x3 box contains each digit 1 to 9 exactly once. Digits outside indicate that they are the largest/smallest of digits (without repetition) across all 9 cells in the same position of their respective box. However, the position of the digit is to be determined.

Puzzle 402: Casino Sudoku

A new sudoku variation.

Rules:   Place a digit in each cell, such that every row, column and 3x3 box contains each digit 1 to 9 exactly once. A pointer is placed in some cells, with direction given. Spin the pointer clockwise as many times as the number placed in the cell. Each rotation is equivalent to a movement of 45 degrees. The final direction pointed to, contains at least one instance of the digit in that cell.

Puzzle 401: Easier than ABC when not alone

This is a new variation to Easy As ABC. I am presenting an example, followed by a 6x6 puzzle.

Rules: In addition to usual rules, every letter has to be adjacent with at least one letter. 

Puzzle 400: 4x100 4-in-one

This is a loop traversing four quadrants while satisfying the corresponding ruleset within each quadrant. The following four puzzle types are involved, rules described below.

Ripple Loop: Draw a closed loop that connects the centres of all cells horizontally or vertically. Wherever two circles are edge-adjacent, the loop must go straight through one, and make a right angle turn in the other.

Balance Loop:  Draw a closed loop passing through the centres of cells horizontally or vertically. All white circles must have equal segment lengths on both sides of the circle before turning. All black circles must have unequal segment lengths on both sides of the circle before turning. Numbers indicate the sum of the segment lengths on both sides of the circle.

Masyu: Draw a closed loop connecting the centres of some cells horizontally or vertically. All circles must be visited. The loop may not intersect itself. The loop has to go straight through every white circle, and
make a 90 degrees turn in at least one adjacent cell, while it has to make a turn in every black circle
and go straight through both cells adjacent to the circle.

Syuma: Draw a closed loop connecting the centres of some cells horizontally or vertically. All circles must be visited. The loop goes straight through every white circle, and turns in every adacent cell. The loop makes a
90 degrees turn in every black circle, and goes straight through at least one of the adacent cells.

Edit: A circle added in R12C8, and R9C7. White Circle in R19C12 in the first version is now corrected to black.

Puzzle 399: Ripple Loop

This ripple loop is a little trickier than the one I had posted a few days ago.
The next puzzle ( puzzle 400) would be 4 puzzles rolled into one. Will be posted soon.

Rules:Draw a closed loop that connects the centres of all cells horizontally or vertically. Wherever two circles are edge-adjacent, the loop must go straight through one, and make a right angle turn in the other.

Puzzle 398: Balance Loop

Rules: Draw a closed loop passing through the centres of cells horizontally or vertically. All white circles must have equal segment lengths on both sides of the circle before turning. All black circles must have unequal segment lengths on both sides of the circle before turning. Numbers indicate the sum of the segment lengths on both sides of the circle.

Theme: shaped by white circles
Edit: A circle  added  in R5C6.

Puzzle 397: Rekuto

Rules: Divide the grid into rectangular regions without overlapping, each containing exactly one number, which indicates the sum of both sides of the region in cells.

Puzzle 396: Regional Loop

Rules: Draw a closed loop passing through centres of all cells horizontally or vertically. The loop passes straight through all circled cells. The number of turns the loop makes in every visited region is constant across the grid.

Edit: The loop visits all cells. This was not mentioned in the ruleset.

Puzzle 395: Syuma

Rules: The loop turns in every black circle and goes straight through at least one adjacent square. The loop goes straight through every white circle and turns in both adjacent squares.

Theme:  almost antisymmetric

Puzzle 394: Masyu

Rules: Draw a closed loop connecting the centres of some cells horizontally or vertically. All circles must be
visited. The loop may not intersect itself. The loop has to go straight through every white circle, and
make a 90 degrees turn in at least one adjacent cell, while it has to make a turn in every black circle
and go straight through both cells adjacent to the circle.

Puzzle 393: Ripple Loop

This is the last puzzle I am posting for the WPC participants looking for some practice. I wrote three ripple loops. I am posting the elementary one here. Other two are a bit tricky.

Rules: Draw a closed loop that connects the centres of all cells horizontally or vertically. Wherever two circles are edge-adjacent, the loop must go straight through one, and make a right angle turn in the other.

Puzzle 391-392: Sum Skyscrapers and Double Letter Easy As(Road to Bangalore)

The WPC opens with a Sum skyscrapers puzzle. Double Letter Easy As is also part of the same session.
This post contains one example of each of those puzzles.
1. Sum Skyscrapers:
Considering the points allocation, and my guess on the theme being potentially nearly similar to what I have used here, I think the WPC puzzle has to be a 7x7.
Rules:Place a digit from 1 to N, in an NxN grid, into each of the empty cells so that each digit appears exactly once in each row and column. Each digit inside the grid represents the height of the skyscraper in that cell. Each number outside the grid represents the sum of heights of skyscrapers that can be seen in the corresponding row or column. Taller skyscrapers hide shorter ones.

2. Double Easy As :
Again, I suspect this theme might be used, based on the points given to that puzzle.
Rules: Place the letters from the given word in the grid, such that each row and each column contains all the letters. Letters must be used as many times as they appear in the word. Identical letters can’t touch each other by a side. Some cells in the grid will remain empty. Letters on the outside indicate that this letter is seen first in the corresponding row or column when looking from that direction.

Edit: This had two solutions in the far-left. Modified to address that.

Puzzle 390: Balance Loop

I had never considered writing a balance loop until now. This is a triple-themed balance loop - no clues on the edges, antisymmetry, and odd clues on blacks, even on whites.

Rules: Draw a closed loop passing through centres of cells horizontally or vertically. All white circles must have equal segment lengths on both sides of the circle before turning. All black circles must have unequal segment lengths on both sides of the circle before turning. Numbers indicate the sum of the segment lengths on both sides of the circle.

Edit: A number added to R6C4, and a circle added to R6C3, to fix uniqueness issue.

Puzzle 387-389: Rassi Silai, Rectangular numbers, Falling Letters

This post contains three puzzles, all of which are appearing in the same session at the WPC. You may want to try these to get some practice.

1. Rassi silai
A simple path puzzle where construction relies on choosing shapes that restrict subpaths within the shape, while not making the puzzle look too trivial. I think this is one of those puzzles which are expected to be solved by every participant.

Rules: Thread a rope in each region. A rope is a path that passes through all cells of the region, between two cells that are end-points. Endpoints don't touch each other, not even diagonally.

2. I suppose "Falling letters" has something to do with the direction most of the competitors are flying to attend the WPC.
The puzzle I posted here would be my first. There is a key connectivity logic in the central 'T' region, otherwise there is nothing much going on.
Rules:
Place letters into some cells in the grid. Same letters cannot share a side, and blank cells cannot share a side. Each outlined region must be filled in alphabetical order, starting with ‘A’, from left to right and top to bottom. Each outlined region contains at least one blank cell. Cells with the letters form a single connected area.

3. Rectangular numbers was conceptualized by someone from India.
Rules: Place any one number from 1 to 4 exactly once in each of the thickly outlined regions. Every row and column must contain either no number, or two instances of the same number. Numbers cannot be placed in black cells. Rest of the Shading is inconsequential to the solution.

Puzzle 386: Nurikabe/Mochikoro

One of the parts in the deception round at the upcoming WPC features nurikabe, mochikoro, and 2 other puzzles that are interrelated in some ways. The puzzle in this post however is a single grid, and is solvable as both a nurikabe, and a mochikoro.

Puzzle 385: The Largest Number

With many better ideas to choose from(my submissions), this was a surprise third puzzle to be included in that round, while the other two seemed to be deserving. Wonder where it would have scored higher than others.
I was trying to write one that is 'acceptably' immune to uniqueness deductions, which I think takes an effort with this and a few other number placement puzzles. The first attempt had two places where you could exploit uniqueness, will post that some other time. In the one I am posting now, it might not be easy to see any uniqueness shortcuts unless one really looks out for.

Rules: Fill every outlined region with different numbers from 1 to N, where N in is the number of cells in the region. No two adjacent cells can contain the same number. No two cells from different regions sharing a side can both contain the largest number of their corresponding regions.

 

Puzzle 384: Joker

This is a reject from the Puzzle Innovations Contest. This and other rejects were new variations around known puzzle styles, and they were not looking for such submissions.

Rules: Divide the grid along the gridlines into some regions, and fill each of the empty cells with a number, or a joker. When two cells containing the same number touch along an edge, they may not belong to different regions. Given numbers represent the area of the region they belong to. A region may contain none, or one or more of the given numbers, and may only contain either one, or no joker. In addition to the given jokers, you may insert more jokers. If a region contains a joker, its size increases by one, and it has to contain at least one number, but the numbers written inside the region do not get incremented. So, an m-omino remains an m-omino, with area m+1.

Puzzle 383: Reachability

Rules: Draw paths from each each arrow such that all cells of the grid are visited by paths. A path can move only into the cell that is pointed at by the arrow, and then moving through the centres of cells horizontally or vertically. A path can visit either four or five cells including the cell with the arrow. Blue line has to be a part of one of the paths.

Puzzle 382: Statue Park

This is a statue park.

Edit: Modified fpr uniqueness.

Theme: Anti-symmetry

Puzzle 381: Fillomino

This is a fillomino.

Theme:  Robot

Puzzle 380: Summon

Rules: Place digits 1 to 3 in some cells, such that every outlined region contains all digits exactly once.
Same digits cannot touch each other, not even diagonally. Connected blocks of digits form numbers
reading across or down. Numbers outside indicate sums of all such numbers in the corresponding
row or column.

Puzzle 379: Tapa

This is a tapa.

Puzzle 378: Cave

 This is a cave/bag puzzle.

Puzzle 377: Pentominous

This is a pentominous puzzle.

Theme: Puzzlers' names.

Puzzle 376: Nanro

This is a Nanro.

Puzzle 375: Rugged terrain

This is a new puzzle style.

Rules: Some numbered Range rovers are placed in the grid. The objective is to drive each car as many cells as the number written in the cell, moving only horizontally or vertically. Shaded cells represent blocks of water. When a car enters water, it has to travel the entire block before leaving. Every cell is visited by exactly one car.

Puzzle 374: Nuraf

Rules: Apply nurikabe rules, except that each island contains two numbers, and the area of the island is a value strictly between those two numbers.

Puzzle 373: Streets and Squares

A nikoli type.

Rules: Paint some empty cells black. Black cells strictly form squares. Unpainted cells are orthogonally contiguous. Clue cells share side(s) with at least one painted square. If the clue contains a number, that is the total area of orthogonally adjacent black squares.

Puzzle 372: Pentoids with Triminoes

Rules: Place some triminoes, such that all 12 pentomino shapes are formed ( shaded cells included). Pentominos cannot touch each other, not even diagonally. Pentominos can be rotated and reflected. Black cells cannot be used.
Edit: Black cell added to eliminate an ambiguity in row 8.